Introduction
As an undergraduate at Cornell, I was fortunate to have been mentored by Professor Francis Moon on the Vibro Wind Project. This project proposes to put panels of about 250 four-inch oscillators per square meter on the sides of buildings. The arrays employ piezoelectric cantilevers to directly power applications or charge batteries. It has been estimated that the arrays can output up to 54 W/m^2, a number that is comparable to the 60-100 W/m^2 output of commercial solar panels.
What makes Vibro-wind unique from other renewable energy sources is that it allows energy harvesting in wind speeds as low as 2 m/s, whereas large-scale wind turbines require at least 9 m/s, and it works in locations with little sun. Furthermore, while some current wind turbine and solar panel designs spark objections from neighbors who consider them eyesores, Vibro Wind's design is based on kinetic sculptures. The image of colored blocks waving in the breeze is inherently beautiful. As exemplified by the New York Time's selection of Vibro Wind as one of the Top Ten Ideas of 2010, the public is strongly willing to embrace the concept.
Click here to see the New York Times 10th Annual Year in Ideas Feature on Vibro Wind
Video of a Vibro-wind array
My project role
As an undergraduate researcher for the project from January 2011 to August 2012, I worked on all aspects of the project and led the undergraduate team from September 2011 to June 2012. I led the team to run wind tunnel tests comparing power output to windspeed, improve the circuittry, and fabricate and test new arrays.
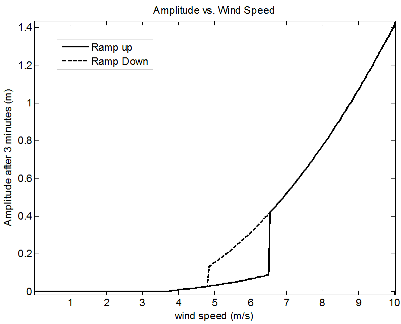
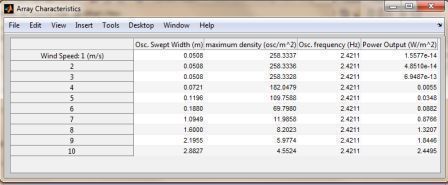
During my senior year (September 2011-August 2012), I worked on a MATLAB program that simulates the motion of oscillators in the wind, their power output, and the energy they store in a capacitor. The program allows the uder to specify the cantilever thickness, length, and blunt body shape. These parameters affect the oscillator stiffness, damping, and galloping aerodynamic coefficient, which, in turn, affect its oscillating frequency and amplitude. Oscillator power increases as oscillator frequency and amplitude increease, but the number of oscillators that fit in a given area decreases with the increasing amplitude. Therefore, an oscillator with an optimal geometry will maximize the array's power output. This program determines the optimal oscillator geometry. Below are images of the program outputs.
I worked with Prof.s Francis Moon and Richard Rand to use the computer algebra software WxMaxima to analytically solve the nonlinear differential equation of motion of an oscillator. The solution could then be maniulated to choose geometry that minimizes hysteresis, minimizes the critical wind speed required for the blunt body to begin oscillating, and maximizes the power output.
I published the paper Shape optimization of a blunt-body Vibro-wind galloping oscillator based on this work.
|
| Array power output for different wind speeds |
|
|
|
|