Challenge

• Ambient vibrations are stochastic multi-frequency, and time-varying.
• Traditional linear oscillators can only absorb ambient energy at one frequency.
• Example scenarios:
• • Ambient vibration energy harvesting
  • • Cell phones carried by people.
    • Ocean wave utility-scale generators.
    • Small electroincs in remote locations.
    • MEMs sensors implanted in the body.
  • Shock absorption
  • • Protect offshore platforms from water wave impacts.

Solution

• Nonlinear oscillators are more robut to vibration signal changes than linear systems
• • Many studies have shown that energy absorption by a nonlinear system depends more on the energy level of the ecxitation signal than the frequency of the excitation signal.
• Traditional linear oscillators can only absorb ambient energy at one frequency.
• • This is a pasive solution which may be more robust and energy-efficient than using controls.

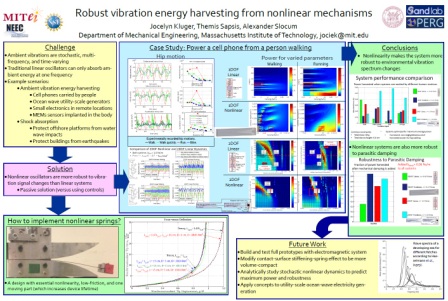
Design a nonlinear spring

• We design an essentially nonlinear spring (i.e. its entire force-versus-deflection behavior is nonlinear), which many studies have shown to be critical for generating power over a large range of excitation signals.
• The chosen design has low friction and only one moving part (which increases device lifetime).
• The spring stiffness increases as the cantilever wraps around the rigid surface and shorter length of the cantilever is able to bend.
• • The stiffness of a cantilever is 3EI/L^3. Here, L decreases as additional force is appled.

Case study: Power a cell phone from a person walking

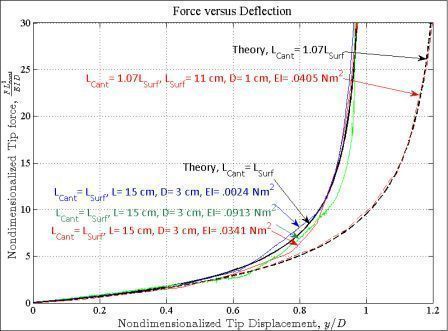
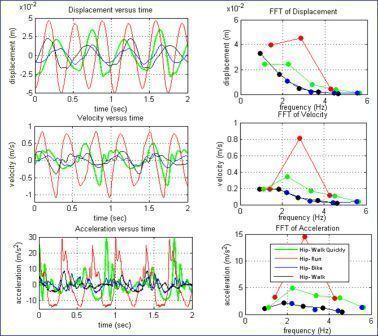
• We study the electricity generated by an energy harvester that is excited by the motion of a person's hip while walking, walking quickly, and running.
• These different excitation signals represent how a person walks differently thorughout the day
• We restrict all of the systems to have a total mass of 60g (for the 2DOF systems, each mass is 30 g), and allowable peak-peak displacement of 6.8 cm. This displacement constraint represents the device outer casing.
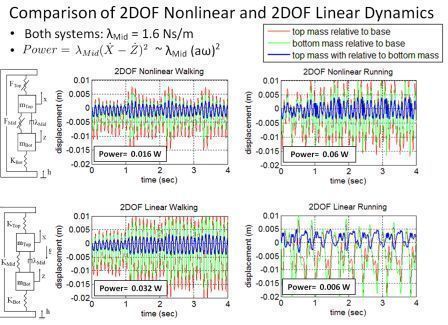
• We simulate the generation of electricity by adding electromagnetic damping to the system.
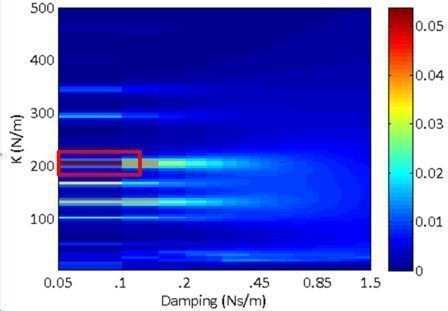
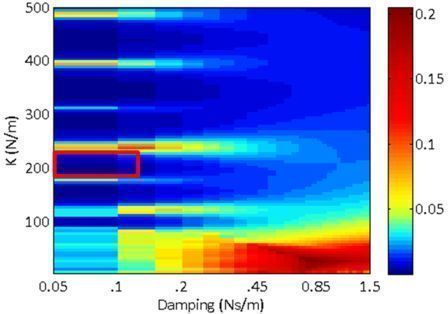
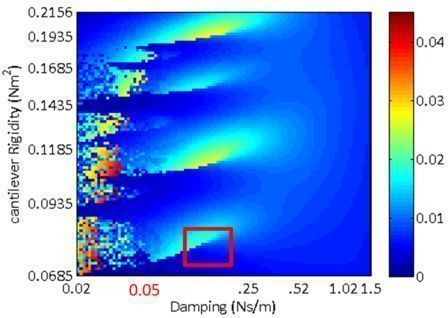
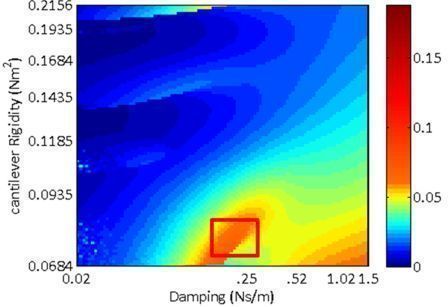
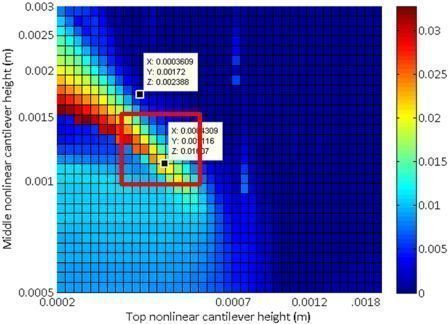
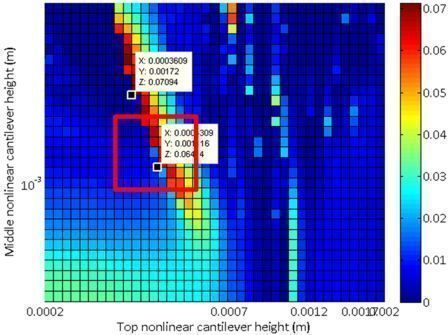
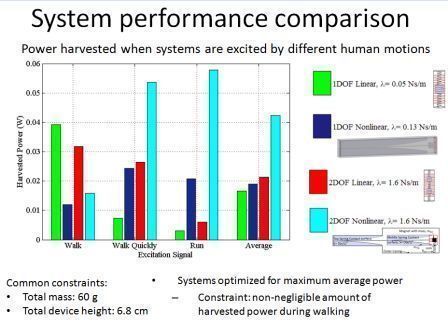
• As shown below, only the nonlinear systems have a set of parameters that can generate a significant (>0.01 W) power for both walking and running.

Times series and FFTs of the human motion signals

System	Power Generated while Walking versus Parameters	Power Generated while Running versus Parameters
1DOF linear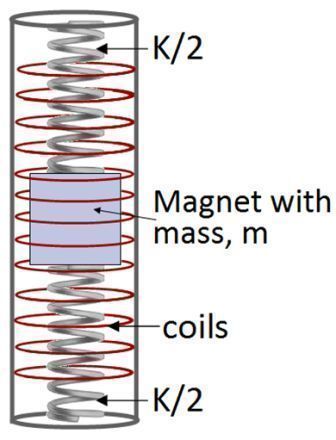
1DOF nonlinear
2DOF linear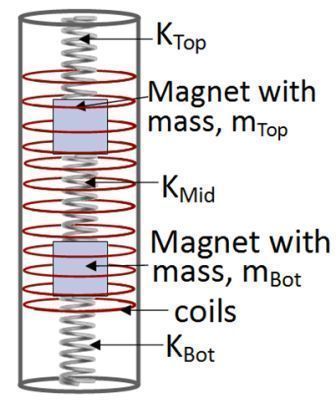
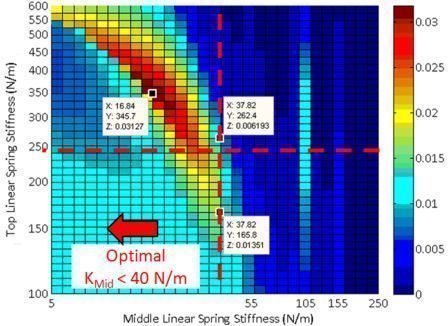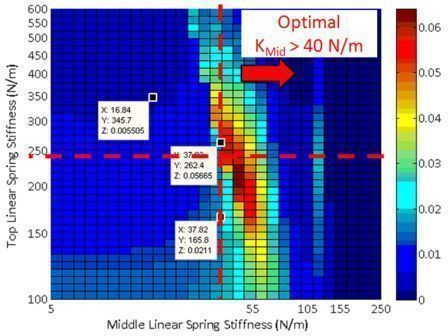2DOF nonlinear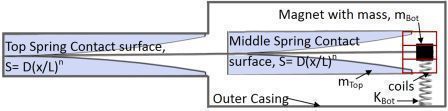

 

Time series of the optimal 2DOF systems. We note that the 2DOF nonlinear system is robust to the different excitation signals while the linear system is not.

Conclusions

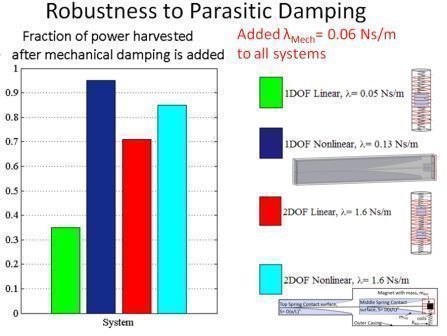
Nonlinearity makes the system more robust to environmental vibration specturm changes and the presence of parasitic damping.

Power harvested by the optimized systems

Effect of parasitic damping

Future Work

• Build and test full prototypes with electromagnetic system
• Modify contact-surface stiffening-spring effect to be more volume-compact
• Analytically study stochastic nonlinear dynamics to predict maximum power and robustness
• Apply concepts to utility-scale ocean-wave electricity generation

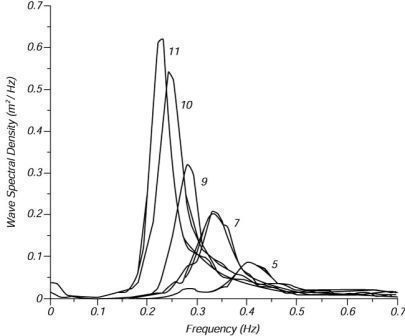
Ocean wave spectra of different sea states, from Hasselmann?et al., (1973)